 Robo Instructus devblog
Robo Instructus devblog
Updates on the development of coding puzzler Robo Instructus
Rust And OpenGL In Orbit
Hi there! My name is Alex Butler and until recently I was a senior enterprise programmer working in London mega-corps. I say ‘until recently’ because in April I decided to leave and try my hand at creating my very own PC games. In this post I’ll show you one of my prototype efforts in the last couple of months; using Rust & OpenGL to render a somewhat interactive gravitational orbit sim.
This post is going to be a bit technical I’m afraid since this is a prototype there isn’t much else to it! In future I’ll be concentrating more on actual games with the maths pushed back into a dark corner.
Why Use Rust?
I’m writing my own engine code (yeah I know, what a silly billy), so I need a fast language with deterministic memory management. I also wanted to avoid C & C++. Rust while young, really fits the bill.
Why Use OpenGL?
While Vulkan is shinier, OpenGL (I used 3.3) is currently best supported on all platforms. And since I’m doing 2D it shouldn’t be too limiting. Also I can change / add additional rendering support on top of OpenGL if necessary.
The Concept
The demo will be pseudo-gravitational bodies orbiting. This means I need to render some circles on the screen and move them around with some gravity maths. I actually started modeling my data on the Earth and the Sun, but I ended up with a tennis ball about a mile away from a pea. So forget the real world, I’ll be rolling my own gravitational constant of the Alexverse.
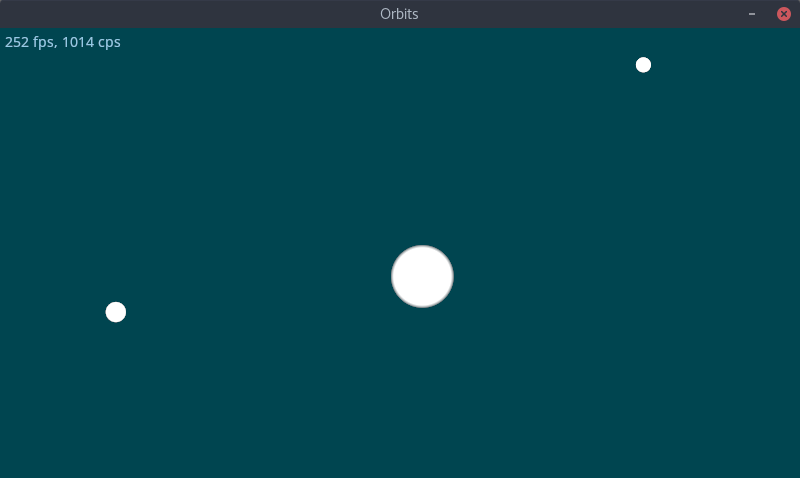
The thing about OpenGL is, it’s just really fond of triangles. To the point where if it isn’t a triangle OpenGL is frankly not interested. To keep my rendering API happy I decided to render the circles you see above using a single triangle. Specifically, an incircle of an equilateral triangle.
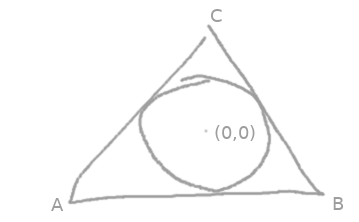
With a bit of geometry chops, we can work out that a radius 1 incircle will have co-ordinates:
A = (-6 / 2√3, -1), B = (6 / 2√3, -1), C = (0, 2)
So that gives us the vertex coords. We can use a OpenGL fragment shader to discard any pixels outside the incircle:
#version 330 core
in vec2 model;
out vec4 out_color;
void main() {
float dist = pow(model.x, 2) + pow(model.y, 2);
if (dist > 1.0) {
discard;
}
out_color = vec4(1.0, 1.0, 1.0, 1.0);
}
Wow, learning Pythagoras’s theorem back in school wasn’t for nothing after all! I can use a single cheeky matrix to perform any positioning and scaling of the individual bodies I want to render. I actually add a little alpha logic to the shader in the real code because I hate aliasing, but it really isn’t much more complex.
So I can draw nice circles now to represent my orbital bodies, and my compute logic is working so the bodies go round each other following gravitational simulation. Nice.
In the next post I’ll look at some of the other demo features: I.e. basic user interactions; zooming, panning, following bodies and perhaps orbital path rendering.
If you fancy you can checkout and run the source yourself, find it at github.com/alex-butler-games/prototype-orbit.